追加武器攻撃力ランダム
予想編
追加武器攻撃力ランダム(以下運補正)とは、運が高ければ高いほど、武器攻撃力の中で高い補正が選ばれる確率が高くなるというものです。
ただし、表記ミスの可能性もないわけではないので、”追加表記ダメージランダム”などといった可能性も否めませんが、いずれにしても防御計算前に補正がかかることは間違いないでしょう。
”追加”とありますが、運がいくら高くても、相手防御0で表記ダメージを超えることはありません。(少なくとも”ほぼ確実に”超えることはありません)
まずこちらをご覧ください。
予想図A
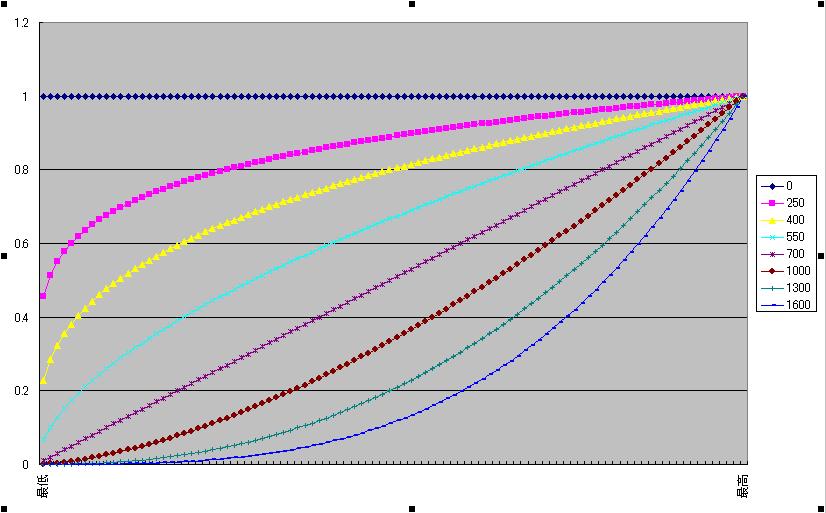
予想図B
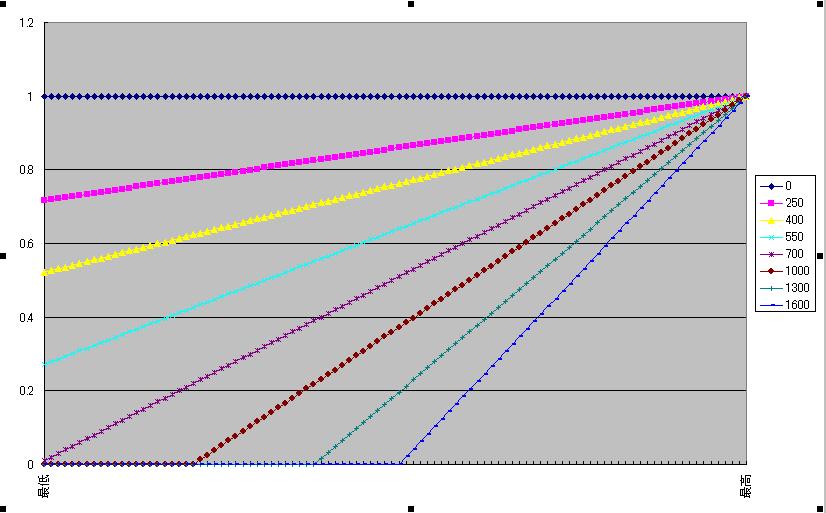
予想図C
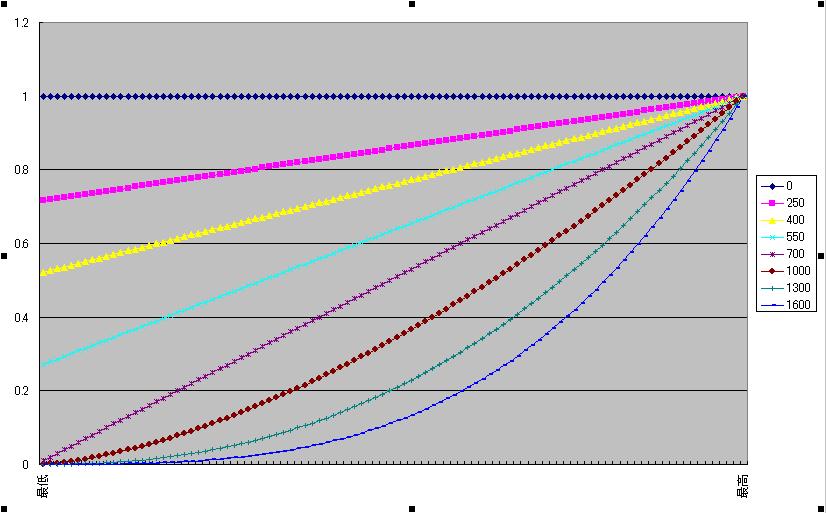
どれも横軸が最低武器攻撃力〜最高武器攻撃力で縦軸が最高武器攻撃力が選ばれる確率を1としたときの確率分布予想図です。
予想図Aはx^a(運による変数)のグラフで、予想図Bはaxのグラフ、予想図Cは予想図AとBの複合型です。
右端の凡例は運の値ですが、数値は適当です。(経験則を元に…)
予想Aのaは運をpとしてlog2(p/800+1)で実際は0,100,200,400,800,1600,3200,6400をとっています。
運がいくら高くても、低確率で低補正が選ばれることがあることから、予想図Bの場合は一定確率もしくは運に一定確率で運補正が無視されるといったようなすっきりしない要素がでてきます。
予想図Aは低運&低補正付近の確率が極端に少なくなるのでこれまたすっきりしません。(どちらも十分ありえますが)
予想図D
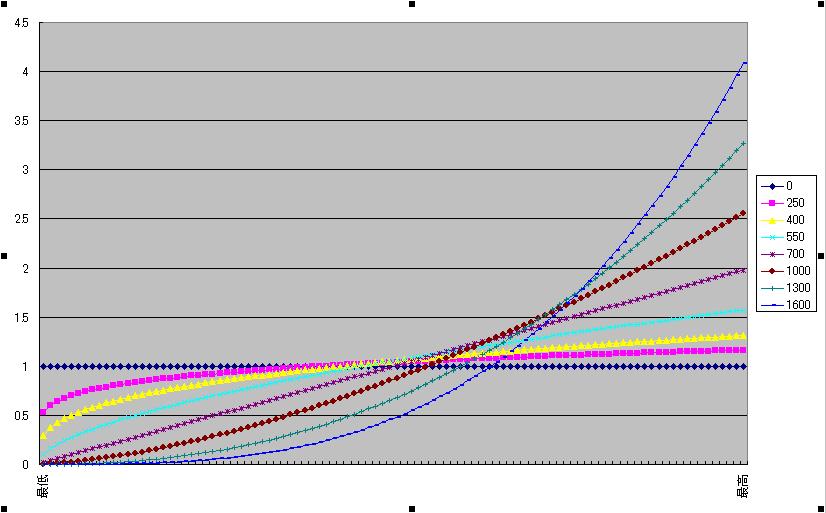
こちらは予想Aの縦軸平均を1としたもの。
さて、上記はいわば結果予想図ですが、そもそも運補正前の武器攻撃力の選定?はプログラム的にはどう処理されているのでしょうか。
恐らく線形合同法もしくはもっと精度の高い擬似乱数アルゴリズムが使われていることでしょう。
プログラミング言語やエクセルに詳しい人ならRAND()やSRAND()といえばわかるはずです。
表記ミスでなく”追加武器攻撃力ランダム”であり、運補正を無視した場合(推定運0)、
r=rand()…0<=r<1の範囲内のランダムに選ばれた値
w=最高武器攻撃力
v=最低武器攻撃力
として、
選ばれる武器攻撃力uは
u=v+(w-v)*r
となるはずです。
※実際は+1されます。
もしかしたら0<=r<=1や0<r<=1や0<r<1かもしれません。
余談ですが、一時期ベースの最高補正がでなかったのは、0<=r<=1でなく0<=r<1になっていたからではないかって噂がありました。
話は戻りまして、これに運補正の要素を加える場合、
相手防御0でも表記を超えることはありませんので、
r'=運補正後のr 0<=r'<1
u=v+(w-v)*r'
であり、rが高いほどr'も高くなり、rが低いほどr'も低くなるはずです。(当たり前だけど…)
これは、予想Aを正しいとしたとき、これを直交座標系にした
f(x)=x^log2(p/800+1)
にxをかけ逆関数にした
r'=x^(1/log2(p/400+2))
x=rであり
予想図E
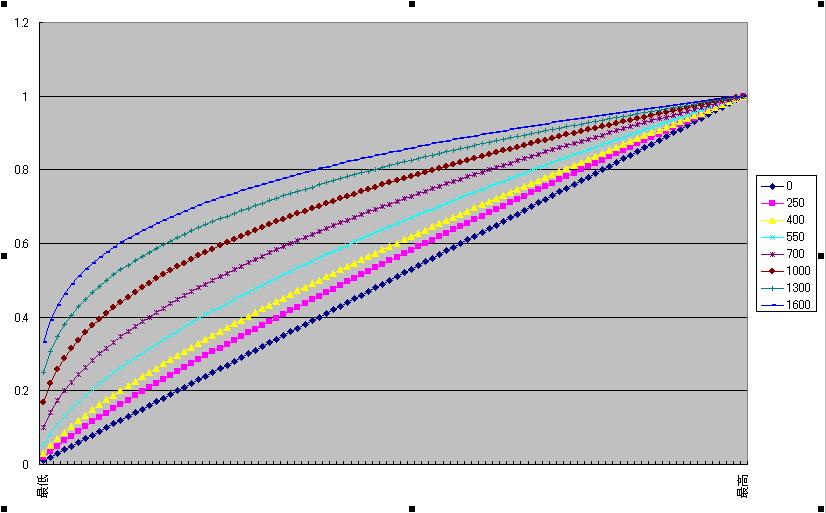
こうなります。
※横軸がr、縦軸が運補正後のr'
ちなみに、この図が正しいと仮定すれば、
運0の補正内の平均武器攻撃力を0.5として
運250 → 0.544140189
運400 → 0.574289204
運550 → 0.618061978
運700 → 0.671462947
運1000→ 0.725634537
運1300→ 0.772891072
運1600→ 0.810494563
となります。
※元データがでたらめなので何の意味もありません。
※防御計算や√計算がありますので、実ダメ平均とは異なります。
とりあえず予想としてはこんな感じです。
あとはデータ取って数字とにらめっこするだけ。(それが大変なのだが…)
トップへ